This page describes (some of) the differences of Welch (4th Ed) and its alternatives. For coverage comparisons, please look at bookcomparison, please.
Innovations in Approach
Every interested and modestly talented student can understand finance. I believe that our finance concepts are no more difficult than those in standard texts covering the principles of economics and that our mathematics is no more difficult than high-school level. I believe that finance is easiest when explained from basic principles and only gradually ramped up in complexity. I also believe that, although it is important for our students to learn how to solve traditional textbook problems, it is more important for them to learn how to think about and approach new problems that they will inevitably encounter in the real world.
A Logical Progression
The book starts with simple and stylized scenarios in which solutions are easy. It then progresses to more complex and realistic scenarios in which questions and answer become more difficult. Within this architecture, chapters build organically on previous concepts. This incremental progression allows students to reuse what they have learned and to understand the effect of each new change in and of itself.
The book has a logical progression from the perfect-market, law-of-one-price ideal world (on which almost all finance formulas are based) to an imperfect market (in which our formulas may need explicit or implicit adjustments).
Numerical Example Leading to Formula
I learn best by following a numerical example, and I believe that students do, too. Whenever I want to understand an idea, I try to construct numerical examples for myself---the simpler, the better. Therefore, this book relies on simple numerical examples as its primary tutorial method. Instead of a ``bird's eye'' view of the formula first and application second, students start with a ``worm's eye'' view and work their way up---from simple numbers to progressively more complex examples. (Formulas are below the numbers.) Each step is easy. At first glance, you may think this may be less ``executive'' or perhaps not as well-suited to students with only a cursory interest in finance, but I assure you that neither of these is the case.
Critical questions such as, ``What would this project be worth?'' are answered in numerical step-by-step examples, and right under the computations are the corresponding symbolic formulas. I believe that the pairing of numerics with formulas ultimately helps students understand the material both on a higher level and with more ease.
Problem Solving
A corollary to the numbers-first approach is my belief that formulaic memorization is a last resort. Such a rote approach leaves the house without a foundation. Instead of giving students too many canned formulas, I try to teach them how to approach and solve problems---often by discovering the methods themselves. I want students learn how to dissect new problems with basic analytical tools.
Self-Contained
Many students come into class with a patchwork of background knowledge. Along the way, holes in their backgrounds cause some of them to get lost. Not realizing when this happened, student frustration rises. I have therefore tried to keep this book largely self-contained.
For example, all necessary statistical concepts are integrated in Chapter~8 (Investor Choice: Risk and Reward), and all necessary accounting concepts are explained in Chapter~14 (From Financial Statements to Economic Cash Flows), though this is neither a full statistics or accounting textbook.
Reasonable Brevity
This book has a count of about 650 pages rather than 1,100 pages. Sometimes, less is more.
Innovations in Content and Perspective
This book also offers numerous topical and expositional innovations, of which the following is a limited selection.
A Strong Distinction between Expected and Promised Cash Flows
I clearly distinguish between the premium to compensate for default (credit risk), which is introduced in Chapter~6 (Uncertainty, Default, and Risk); and the risk premium, which is introduced in Chapter~9 (Benchmarked Costs of Capital). Students should no longer mistakenly believe that they have taken care of credit risk by discounting a promised cash flow with a CAPM expected rate of return. (If they commit this error---and I know from painful experience before writing this book that many students of other books do---it would have been better if they had never taken a finance course to begin with.)
More Emphasis On Term Premia, Even in Equity Premia
There are many ``nuances'' in calculating and assessing term and equity premia. Some methods are clearly correct, others incorrect. For example, should one use geometric or arithmetic rates of return? Short-term or long-term bonds? These choices induce large differences in inference, even for benchmarked cost of capitals. Should one use 50 or 100 years when estimating forward from historical premia. And this is even when based on the same historical data. For example, one can quote as high an estimate as 8% or as low an estimate as 2%. Mistakes here one dwarf errors that the CAPM commits, and we can explain and get this right! See Chapter~9.
Relative Deemphasis of the CAPM
Every student needs to understand the CAPM because it is a finance standard. This book explains it well.
However, the empirical evidence is clear: the CAPM is not even a good approximation and even in its most common use form. It takes little sophistication to understand this. Figure 10.3 on page 226 shows it.
Moreover, its most common input assessments make no sense in the context of long-term capital budgeting. Clearing them up helps the model commit less serious mistakes. (Levi-Welch, JFQA, April 2017 discuss best practice in more detail.)
- As in the benchmarking approach, it is first-order important to assess a good equity premium. Did you know that from 1970 to 2015, stocks outperformed long-term Treasury bonds by about 2% per year. Really. See Figure 9.3 on page 197.
- Forecasting an equity beta over 5-20 years is hard. Beta estimates require much more a-priori shrinkage than is common. This is not due to estimation uncertainty, but due to changing betas even in the historical data estimation sample. Step back and ask yourself---do you really think we have a good model that can predict which stocks will do better than others over time frames of years or decades? This exercise seems largely futile.
So why are other textbooks still perpetuating this fairy-tale model in chapter over chapter, while glossing over what really matters?
Robustness
The book describes what finance practitioners can reasonably know and what they can only guess at (with varying degrees of accuracy). In the application of a number of financial tools, I point out which of the guessed uncertainties are likely to have important repercussions and which are minor in consequence. I also try to be honest about where our academic knowledge is solid and where it is shaky.
A Spotlight on the Pitfalls of Capital Budgeting
A self-contained chapter (Chapter 13: Capital Budgeting Applications and Pitfalls) describes real-world difficulties and issues in applying capital budgeting techniques, ranging from externalities to real options, to agency problems, behavioral distortions, and so on. The chapter ends with an ``NPV Checklist.''
Comparables
A chapter on comparables (Chapter 15: Valuation from Comparables and Some Financial Ratios), usually not found in other corporate finance textbooks, shows that if used properly, the comparables valuation method is a good cousin to NPV.
Financials from a Finance Perspective
A self-contained accounting chapter (Chapter 14: From Financial Statements to Economic Cash Flows) explains how earnings and economic cash flows relate. When students understand the logic of corporate financial statements, they avoid a number of common mistakes that have crept into financial cash flow calculations ``by tradition.'' In addition, a synthesizing chapter on pro formas (Chapter 21: Pro Forma Financial Statements) combines the ingredients from previous chapters---financials, comparables, capital budgeting, taxes, cost of capital, capital structure, and so on. Many students will be asked in their future jobs to construct pro formas, and our corporate finance curriculum has not always prepared them well enough to execute such assignments appropriately and thoughtfully.
An Updated Perspective on Capital Structure
The academic perspective on capital structure has been changing. Here are a few of the more novel points emphasized in this book:
- Corporate claims do not just have cash flow rights but important control rights as well. This fact has many implications---even for one common proof of Modigliani-Miller.
- Unless the firm is close to financial distress, it probably does not matter much how the firm is financed. Project choice is likely to be far more important than the debt-equity choice. (This does not mean that access to financing is not important, just that the exact debt-equity mix is not.)
- Corporate liabilities are broader than just financial debt. In fact, on average, about two-thirds of firms' liabilities are nonfinancial. The firm value is thus the sum of its financial debt and equity plus its nonfinancial debt (often linked to operations). Again, this can be important in a number of applications.
- Adverse selection causes a pecking order, but so do other effects. Thus, the pecking order does not necessarily imply adverse selection.
- The debate about trade-off theory has moved to how slowly it happens---whether it takes 5 or 50 years for a firm to readjust.
- Historical stock returns are a major determinant of which firms today have high debt ratios and which have low debt ratios. A simple inspection of the evolution of Intel's capital structure from 2013 to 2015 in Chapter 16 makes this plainly obvious.
- Capital structure may not necessarily be a corporate-control device. On the contrary, equity-heavy capital structures could be the result of a breakdown of corporate control.
- Preferred equity and convertibles have become rare among publicly traded corporations over the past decade.
- A novel synthesizing figure (Figure 19.5 on page 542) provides a conceptual basis for thinking about capital structure in imperfect markets. It shows how APV fits with other non-tax-related imperfections.
Specific Changes for the Fourth Edition
This edition has been updated to 2017. The one major change is the insertion of Chapter 9 (Benchmarked Costs of Capital), and the just-discussed even more skeptical view about the practical usefulness of the CAPM. There are small changes throughout the book, but this book is deliberately converging to the clearest explanations. After all, unlike my peers, I do not need to suppress resales via new editions. There are no changes for the sake of changes.
Superior Course Website
syllabus.space provides a superior online course site for your students. The following shows an example equiz question the way a student would see it. The numbers in the questions change every time the quiz is refreshed. Thus, a student can take the same question many times! Nicely formatted math online is no problem, either. Nice?
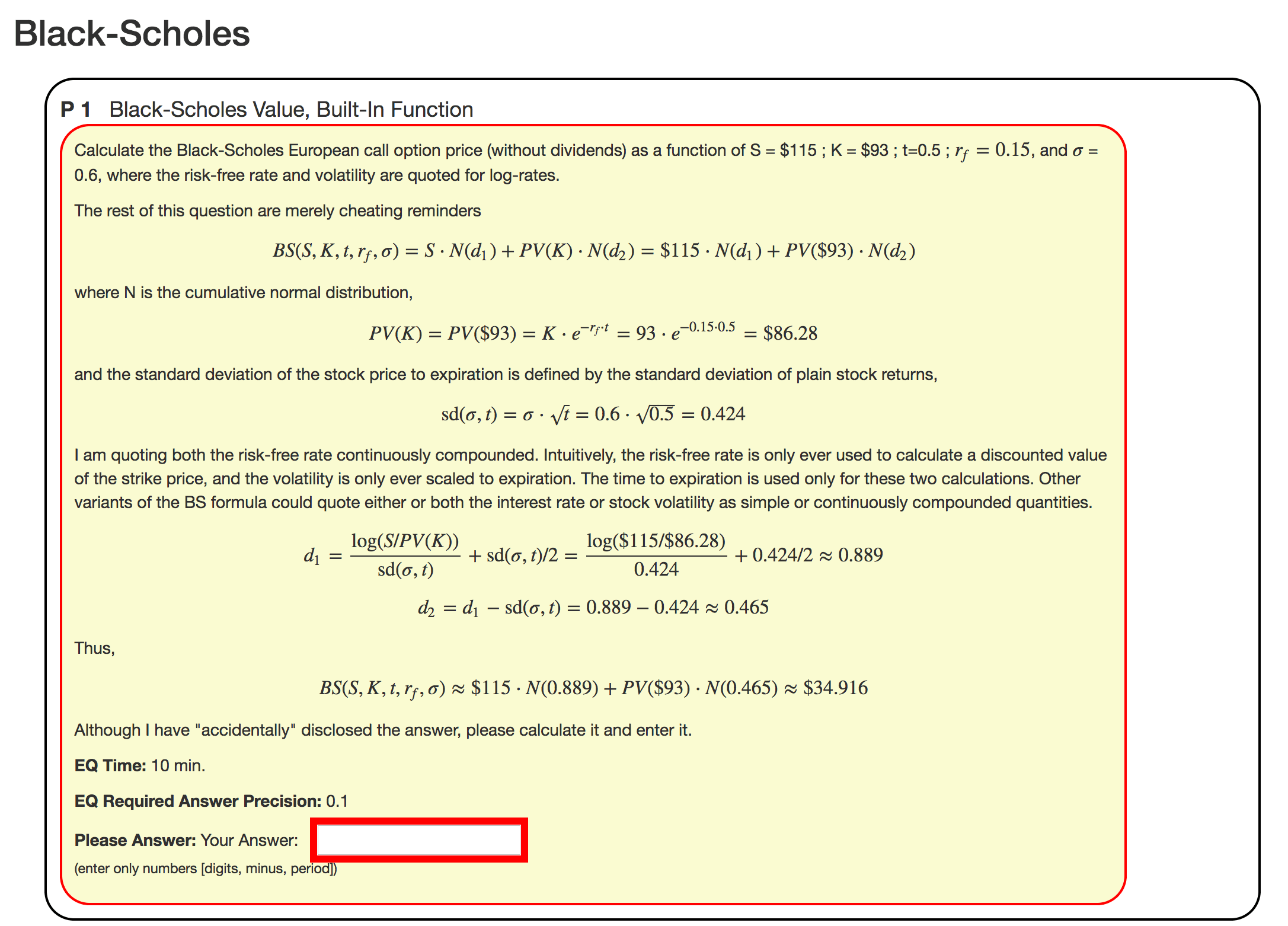
But it gets (much) better. Instructors can easily edit quizzes, and with numerical values that change with each browser refresh! For example, the above question was written as follows. First, ::I:: initializes variables (here, $S to a randomly drawn integer between 100 and 120; $rf to either 10%, 15%, or 20%; etc.), calculates values, and calculates the most important calculation, the answer. The answer must be placed into the special variable $ANS.
:I: $S = rseq(100,120) ; $K = rseq(90,130) ; $t=1/pr(2,4) ;
$rf=pr(0.10,0.15,0.20) ; $sd= pr(0.40,0.50,0.60) ;
$pvk= $K*exp(-$rf*$t); $sdS = $sd*sqrt($t);
$d1 = ( log($S/$K) + ($rf+$sd^2/2)*$t ) / ( $sd * $t^0.5 );
$d2 = $d1 - $sd * $t**0.5;
$ANS= BlackScholes($S,$K,$t,$rf,$sd)
Next, ::Q:: poses the question itself to the student. To nicely format questions, we want to use html tags like <p> (e.g., for paragraph separation or bold display), and we want to use latex-style formulas (like \frac{\sigma\textasciicircum2}{2} to show mathematical notation. Can this really all work together? Yes!}
:Q: Calculate the Black-Scholes European call option price (without dividends) as a
function of S = $ $S ; K = $ $K ; t=$t ; \( r_f= $rf \); and \(\sigma\) = $sd,
where the risk-free rate and volatility are quoted for log-rates.
The rest of this question are merely cheating reminders
\[ BS(S,K,t,r_f,\sigma) = S\cdot N(d_1) + PV(K)\cdot N(d_2)
= \$ $S \cdot N(d_1) + PV(\$ $K)\cdot N(d_2) \]
where N is the cumulative normal distribution,
\[ PV(K) = PV(\$ $K) = K\cdot e^{-r_f\cdot t} = $K\cdot e^{-$rf\cdot $t} = \$ $pvk \]
and the standard deviation of the stock price to expiration is defined by the
standard deviation of plain stock returns,
\[ \mbox{sd}(\sigma,t) = \sigma\cdot\sqrt{t} = $sd\cdot \sqrt{$t} = $sdS \]
I am quoting both the risk-free rate continuously compounded...[deleted]
\[ d_1= \frac{ \log(S/PV(K)) }{\mbox{sd}(\sigma,t) } + \mbox{sd}(\sigma,t)/2
= \frac{ \log(\$ $S/\$ $pvk) }{ $sdS } + $sdS/2 \approx $d1 \]
\[ d_2= d_1 - \mbox{sd}(\sigma,t) = $d1 - $sdS \approx $d2 \]
Thus,
\[ BS(S,K,t,r_f,\sigma) \approx
\$ $S \cdot N($d1) + PV(\$ $K)\cdot N($d2) \approx \$ $ANS \]
Although I just "accidentally" told you the answer, please give it anyway.
(For LaTeX users, the only aspect to keep track of is that a single '$' no longer means starting math-mode, but a variable. Thus $ $x first prints a dollar and then displays the x variable's content. Use \( and \) as the alternative to start and stop inline math. It's better anyway.)
Finally, we need ::A:: to explain the correct answer after the student has submitted her own answer:
:A: The answer was already noted as $$ANS.
\[ BS(S,K,t,r_f,\sigma) \approx \$ $S \cdot N($d1) + PV(\$ $K)\cdot N($d2)
\approx \$ $ANS \]
This equiz system has been successfully used to design quizzes by other instructors for unrelated courses (such as derivatives).
(Optional) Simple Course Administration
Annoyed by (too-)feature-rich but clunky and hard-to-understand course websites? Me, too! The syllabus.space system also offers intuitive course administration functionality for instructors and schools. The learning curve is near zero. For example, look at the following:
What is not immediately clear?
Instructors can receive reports on student equiz performance, post messages, post and collect student homework answers, post syllabi, allow students to see who completes quizzes first (gamification), etc.
The software is all open-source and free for academic non-profit institutions. So any academic department can install the system on their own IT servers, tinker with it, pass it on to other academic institutions, etc. (Commercial textbook publishers, please contact me.)
When instructors want to run their websites on my server, I usually give them their own subdomains, such as mfe327.welch.syllabus.space. At small single-class scale, I can do this easily and without charging. At large scale (1,000 students plus), I would have to hire a dedicated IT expert and charge $20/student.
Other Instructor Materials
Qualified instructors from accredited institutions can receive full support materials. These are not made available to students under any circumstances. If you believe you qualify, please email ivo.welch@gmail.com, noting the class you are teaching and a university webpage that shows your official affiliation. I am not trying to annoy you, but students have tried to masquerade as instructors in the past.
The website also has a map at bookcomparison.html that compares topic coverages across major books. You should switch to this book asap---it is not only free and thus saves students a ton of money, but it is also simple a better book than its peers.